Spin physics and spin qubits
In 2018, for the first time, universal programmable spin-based quantum processors have been demonstrated [1,2]. Both of these independent implementations comprised only two qubits, but they mark an important milestone and starting point for future scaling of the qubit architecture based on electron spins in semiconductor quantum dots [3,4,5]. The universal two-qubit gate in these implementations is a resonant quantum gate [6] that emerges as a consequence of exchange coupling and magnetic field gradients [7]. The currently investigated spin qubits in silicon also interact with their valley degree of freedom which enables alternative paradigms for exchange-based quantum computation [8]. Looking forward, we have recently proposed a new spin qubit architecture, the quadrupolar exchange (QUEX) qubit [9] (see the figure below) which provides protection from both magnetic and electric noise, and which is based on earlier work on exchange-only qubits [10].
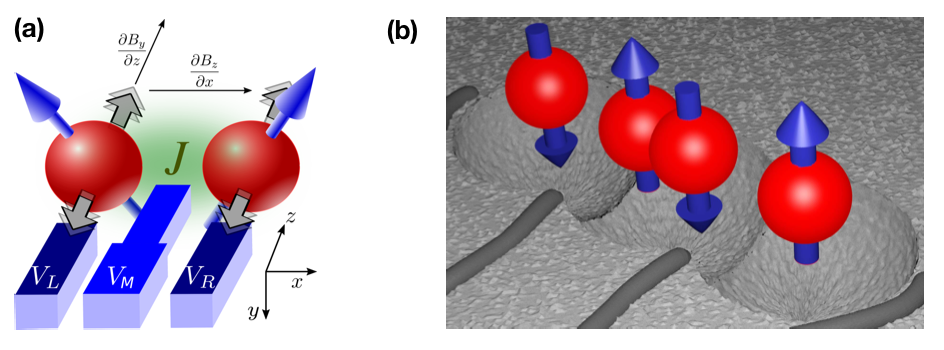
Figure 1 (a) Gate defined double quantum dot (DQD) occupied with two electron spins in a magnetic field gradient. A gradient along the double-dot (x) axis gives rise to distinguishable spin resonance frequencies. Periodic modulation of the gate voltages shifts the electron position in the z direction which generates an oscillating magnetic field in the motion frame of the electrons due to the gradient. An electrostatic barrier gate allows for precise control over the exchange interaction J between the spins. (b) Artist’s impression of an electrostatically defined triple quantum dot (TQD). The four spins are coupled via interdot and on-site exchange interaction. The center dot is occupied by two electrons, giving rise to a large and electrostatically tunable energy splitting.
[1] D. M. Zajac, A. J. Sigillito, M. Russ, F. Borjans, J. M. Taylor, G. Burkard, and J. R. Petta, Science 359, 439 (2018)
[2] T. F. Watson et al., Nature 508, 500 (2018)
[3] D. Loss and D. P. DiVincenzo, Phys. Rev. A 57, 120 (1998)
[4] G. Burkard, D. Loss, and D. P. DiVincenzo, Phys. Rev. B 59, 2070 (1999)
[5] G. Burkard, T. D. Ladd, A. Pan, J. M. Nichol, and J. R. Petta, Rev. Mod. Phys. 95, 025003 (2023)
[6] M. Russ, D.M. Zajac, A.J. Sigillito, F. Borjans, J.M. Taylor, J.R. Petta, G. Burkard, Phys. Rev. B 97, 085421 (2018)
[7] G. Burkard, D. Loss, D. P. DiVincenzo, and J. A. Smolin, Phys. Rev. B 60, 11404 (1999)
[8] N. Rohling, M. Russ, and G. Burkard, Phys. Rev. Lett. 113, 176801 (2014)
[9] M. Russ, J. R. Petta, and G. Burkard, Phys. Rev. Lett. 121, 177701 (2018)
[10] D. P. DiVincenzo, D. Bacon, J. Kempe, G. Burkard, and B. K. Whaley, Nature 408, 339 (2000)
